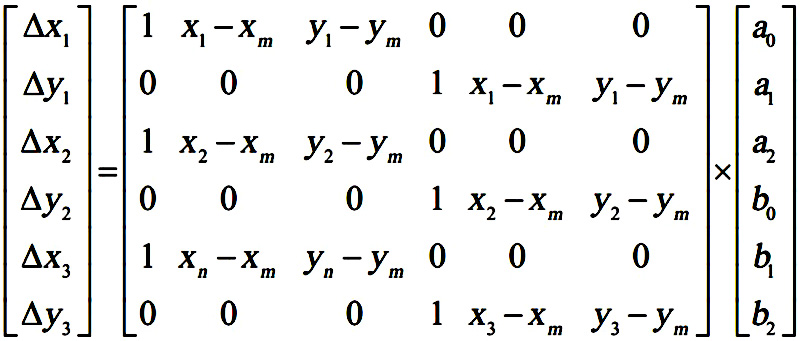مبانی محاسباتی در تحلیل جابجایی سنجی

همان طور که بیان گردید برای تشخیص جابجایی نقاط، از شبکه های آشکارسازی جابجایی استفاده می شود. در این شبکه ها با انتخاب نقاطی که از لحاظ اهمیت جابجایی و نیز پیش آنالیز شبکه ای مناسب باشند، یک طرح مشاهداتی تهیه شده و در دو یا چند اپک این مشاهدات انجام می گیرد. مشاهدات اپک ها باید آنالیز گردد تا بتوان به کمک آنها میزان جابجایی نقاط را اندازه گیری نمود. اما پیش از انجام این آنالیز لازم است تشخیص دهیم کدامیک از نقاط جابجا شده اند و کدام یک نشده اند. ضروری است که در شبکه، نقاطی ثابت داشته باشیم تا بتوان از آنها برای توجیه سیستم مختصات استفاده نمود. اگر چنین نقاطی وجود نداشته باشد ما نمی توانیم ایده ای از جابجایی نقاط در بازه زمانی بین دو اپک داشته باشیم، چون مبنایی برای این اندازه گیری وجود ندارد. اما در واقعیت همیشه کلیه نقاطی که به عنوان مبنا در نظر گرفته شده اند در بازه زمانی مورد نظر ثبات خود را حفظ نمی نمایند و گاها از جای خود حرکت می کنند. لذا لازم است نقاطی از این مجموعه را که از جای خود حرکت نموده اند تشخیص داده و از جمع نقاط مبنا کنار بگذاریم تا باعث ایجاد جابجایی کاذب در نتایج محاسبات نشود.

اما حال مسئله این است که چگونه تشخیص دهیم کدام نقطه حرکت کرده و کدام یک ثابت بوده اند. برای این کار روش هایی موجود است که در ادامه به آنها خواهیم پرداخت. یکی از این روش ها روش تست ثبات کلی شبکه (Cooper, 1987) و (Fraser, et al., 1984)، روش دیگر مینیم سازی نرم L1 بردار جابجایی (Chen, et al., 1990)  و روش دیگر بر مبنای سرشکنی همزمان دو اپک مشاهداتی است که توسط آقای علایی (۱۳۹۰) ارائه شده است.

از آنجایی که شرح روش های بیان شده در بالا مفصل می باشد، به ارائه روشی مناسب تر می پردازیم. در روش های بالا مبنای کار نقاط ثابتی می باشند که تعیین کننده توجیه سیستم مختصات هستند. اگر بنا به دلیلی این نقاط ثابت جابجا شوند جابجایی سنجی ما صحت خود را از دست داده و نمی توان جابجایی را بر اساس آنها اندازه گیری نمود. به همین دلیل می بایست سیستمی برای اندازه گیری جابجایی پیاده سازی نماییم که از اثر سیستم مختصات مبرا باشد. برای این کار می بایست مدلی برای جابجایی صورت گرفته تعیین کرد و از روی آن مدل جابجایی های صورت گرفته بر روی جسم را مشخص نمود.

تعیین مدل جابجایی

از موضوعات مهم در ارتباط با آنالیز جابجایی، تعیین تغییر شکل شیء می باشد. این مطلب مستلزم دست یافتن به مدل جابجایی است. برای این منظور مدلی تقریبی برای جابجایی انتخاب کرده، آن را از طریق اطلاعات مربوط به جابجایی نقاط، تصحیح می کنیم. بهتر آن است که مدل انتخابی تابعی از کمیتهای ناوردا باشد تا فارغ از اثر سیستم مختصات به ترمیم و تعیین پارامترهای آن بپردازیم.

مدلی که معمولا تشکیل داده می شود دارای سه مؤلفه است :

• حرکت مستقیم
• حرکت دورانی
• تغییر شکل

جابجایی یک جسم صلب تنها دارای مولفه های ۱و۲ است. اگر میزان تغییرات شکل جسم به بزرگی جسم را مقداری کوچک درنظر بگیریم می توانیم مدل تغییر شکل شیء را بصورت خطی همانند زیر درنظر بگیریم.

 یا در فرم ماتریسی:

در رابطه بالا r بردار موقیت نقطه مورد نظر و d_i جابجایی است که در آینده در موقعیت r بوجود می آید. d₀ بردار حرکت مستقیم و E ماتریسی در ارتباط با دوران و تغییر شکل است.

همانگونه که ملاحظه می فرمایید رابطه ای که بین موقعیت و جابجایی در نظر گرفته شده از نوع خطی است. چرا که عملا مقدار جابجایی نسبت به وسعت منطقه یا عارضه بسیار کوچک است. بنابراین فرض مدل خطی فرضی کاملا منطقی است.

اگر با یک دید هندسی به رابطه قبل نگاه کنیم، E نقش ژاکوبین انتقال از فضای موقعیت به فضای جابجایی است.

حال می توان E را بصورت زیر به دو ماتریس متقارن و پاد متقارن تجزیه نمود.

از طرفی هر دوران کوچک را می توان به صورت مجموع یک ماتریس یکه و یک ماتریس پادمتقارن نوشت. بنابراین می بایست به منزله دوران و S تغییر شکل (Strain) باشد. اگر S و  را بصورت زیر بنویسیم:

آنگاه می توانیم به نتایج زیر دست پیدا کنیم:

تذکرات:

1. e_xy=e_yx است چون ماتریس S متقارن است.
2. S را تنسور استرین نیز می نامند.

برای حل ضرایب a₀ تا b₂ می بایست از روشی به نام روش اجزاء محدود استفاده نمود. همانطور که مشخص است تعداد معدلات ما برای هر نقطه ۲ و تعداد مجهولات ما ۶ تاست. پس برای حل معادلات به حداقل سه نقطه نیاز داریم. برای این کار می بایست کل نقاط سطح شیء را مثلث بندی کرده و از دو نقطه کناری هر نقطه برای حل معادلات استفاده کنیم. در زیر معادلات مربوط به روش اجزاء محدود برای به دست آوردن مجهولات را مشاهده می کنید.

نمایی از یک نود و دو نود کناری آن در روش اجزاء محدود

بعد از برآورد مدل جابجایی تعیین تغییر شکل و دوران حاصل از جابجایی نیز میسر است. از طریق  معادلات بالا می توان عناصر ماتریس دوران جزئی و strain را بدست آورد. با توجه به ماتریس ژاکوبین E در می یابیم که عناصر این دو ماتریس عاری از اثر سیستم مختصات هستند. بنابراین بررسی اطلاعات موجود در آنها  می تواند ما را به سمت نتیجه گیری های صحیحی در مورد جابجایی هدایت کند. براین اساس و با توجه به معادلات و تعاریف بالا، در تعیین جابجایی و تغییر شکل نامگذاری های زیر صورت گرفته است.

با تعیین این کمیت ها می توان به شمایی از تغییر شکل حاصل از جابجایی رسید. در زیر این تغییر شکل ها را مشاهده می نمایید.

تغییر شکل های تحلیل شده حاصل از جابجایی

 منابع

[۱] اسماعیلی، فرید، «بررسی روش های جابجایی سنجی سیستم های حفاظت جداره ترانشه و گود در مناطق شهری و فضاهای محدود با تاکید بر نقش فتوگرامتری»، پایان نامه کارشناسی ارشد، دانشگاه خواجه نصیرالدین طوسی، پاییز ۱۳۸۹

[۲] سعادت سرشت،محمد، «افزایش اتوماسیون روند  طراحی شبکه در فتوگرامتری صنعتی با استفاده از مدلسازی نایقینی قیود دید و جانمایی دوربین »، پایان نامه دکتری، دانشگاه تهران، شهریور ۱۳۸۳

[۳] علایی طباطبایی، سید محسن، «آنالیز پایداری نقاط شبکه­های آشکارسازی جابجایی بر اساس سرشکنی همزمان دو اپک»، پایان نامه کارشناسی ارشد، دانشگاه خواجه نصیرالدین طوسی، ۱۳۹۰

[۴] J. Fryer, H. Mitchell, and J. H. Chandler, “Applications of 3D measurement from images”. Whittles, 2007

[۵] Jiang, R &, V.Jauregue, D. 2010. “Developement of a digital photogrammetric system for bridge deformation measurment” . Las Cruse, New Mexico: New Mexico State University.

[۶] Clive S. Fraser , et al. “ HYPER REDUNDANCY FOR ACCURACY ENHANCEMENT IN AUTOMATED CLOSE RANGE PHOTOGRAMMETRY ” . The Photogrammetric Record 20(111): 205–۲۱۷ (September 2005)